Overview and motivation

It’s hard to pindown in history an origins to optimization, be it the idea or the practice. Arguably, it’s always been with us.

Some could say that, in a way, it’s even an essential part of our behavior - and we’d be always trying to optimize something, albeit frequently unaware of just what that something is. Others would say that, if it isn’t, in a way it ought to be in the mental machinery of the moral being - so, for instance, utilitarians would have the “moral action” to be the one that minimizes suffering (or, depending on your rendering of their idea, to maximize happiness).

Some explicit idea of optimization has certainly been with us for a long time. Centralized nation states had real worries concerning the best way of effecting (say) transportation of grains, especially in warring times (one could look at Sun Pin allusions to this, albeit somewhat vaguely).

Regardless, optimization as an idea has been much more developed with the recent development of abstract mathematics (“recent” meaning from a couple centuries ago), where it enjoyed, and still enjoys central role for the establishing of core (and, at times, surprising) properties of mathematical objects - so, for instance, we have the Simplex method (we’ll come back to it further below) being used to prove a theorem in sphere packing. Also, one might be surprised at the problems that can pretty directly be laid as optimization problems - one simple and well-known example being the one of solving a linear equation \(Ax = b\), that can be set as minimizing \(\frac{1}{2} x'Ax + b'x + c\) for the unknown \(x\) (with \(x'\) standing for the dual of \(x\), often identified with its transpose).

While very important and interesting in their own right, those kinds of uses are seen (more or less rightly) as somewhat ad hoc, hardly generalizable uses of optimization machinery for expressing extremal properties of spaces in question (such as the solution of an equation).

My goal here is pinpoint cases where it is the way around - namely, where optimization machinery enters in a way that seems surprisingly essential to the mather (or maybe, to the way we handle it) that it can hardly be thought as ad hoc, but either as suggesting essential properties of the object, or essential properties in the way we think of the mather. Either way, optimization enters with an essential role in the puzzle.

This first post though is more of an introductory character, where I discourse about some of the most common optimization techniques, some (a little bit) of the history, and their effects, laying the ground for the subsequent discussion.

First steps

First, let’s try to have a more definite idea of what we’re talking about when we talk about “optimization”.

More generally, in order to optimize something, one needs to have a space \(S\), wherein lie objects¹ such as \(x\) and \(y\), that one can compare. It isn’t a priori necessary for any two \(x\) and \(y\) to be comparable (though it’s often the case), so we shan’t ask that.

Mathematically, all that is needed are a set and a preorder² relation. That preorder is commonly given by what’s often termed a “cost function” \(c: S \rightarrow \mathbb R\), and we then say that \(x \preceq y \Leftrightarrow c(x) \leq c(y)\).

I don’t know whether it’s essential that \(c\) lands on \(\mathbb R\). In \(\mathbb R\) one has naturally a total order³, which makes things easy, but I see no a priori reason why it wouldn’t naturally land on a more structured algebraic object. But never mind that for now.

A brief historical detour

Those remarks above might seem silly. Anyone with some mathematical background, upon a few seconds of thought would come to a similar formulation (perhaps in different words) and could be inclined to think it’s scarcely necessary to put it into words. But it is, and it’s important to note that optimization it’s a somewhat new notion. Up to roughly the WWII time, mathematical optimization techniques were mostly used as ad hoc ways to find properties of abstract objects (or constructing them).

That is not to say that there weren’t prior efforts - there were plenty! one could enlist, for instance, Huygens and Pascal when trying to solve problems involving complex decisions by using theory of probability, and Babbage’s research into the cost of transportation and sorting of mail, and later Ford Harris’ research into inventory management. They were mostly disconnected from one another though, and mostly seen as the rational efforts of educated individuals to better some aspect of society, rather than part of some structured theory. But then, roughly at around the 40s, that sort of started changing.

The change materialized in the field that was then (and up to now) named Operations Research (henceforth, OR). OR includes optimization techniques - or, should I rather say, applied mathematical optimization, also referred to as matematical programming, but also adjacent practices, such as mathematical modeling. The “Operations” in the name would really stand for “war operations”, since that was the primary beneficiary of the theory at the time, having had military institutions as their primary financier. Also, the programming in mathematical programming doesn’t stand for computer programming as one might think (mind you, computers weren quite a rare sight at the time), but rather to the programs the military had to propose in logistics and such.

It is an interesting thing to note the tendency people have of starting to take things more seriously only when there is war involved - or, conversely, to say that “it’s war” when they mean to take things more seriously. But never mind that for now, let’s go on with the theory.

Linear Programming

The first widespread method, that was to become of crucial import to (way too many) different fields - from management to solving industrial problems, to more mundane things as the diet problem was the simplex method. It is also one of the simplest optimization methods, and provides good insights into more complicated ones - and ones that are good for other tasks.

The simplex method is a method for solving Linear Programming problems (LP problems) taking the form⁴

\[\begin{split} \text{minimize } & a'x\\ \text{ such that } & Ax \leq b \end{split}\]

where \(x \in \mathbb R^n\), \(a \in \mathbb R^n\), \(A \in \mathbb R^{m \times n}\) and \(b \in \mathbb R^m\). Roughly speaking, the expression \(Ax \leq b\) defines \(m\) inequalities, that materializes in a region of \(\mathfrak R^n\), whereas \(a'x\) gives us the ordering to be effected.

In \(\mathbb R^2\), for instance, we could have something like the following

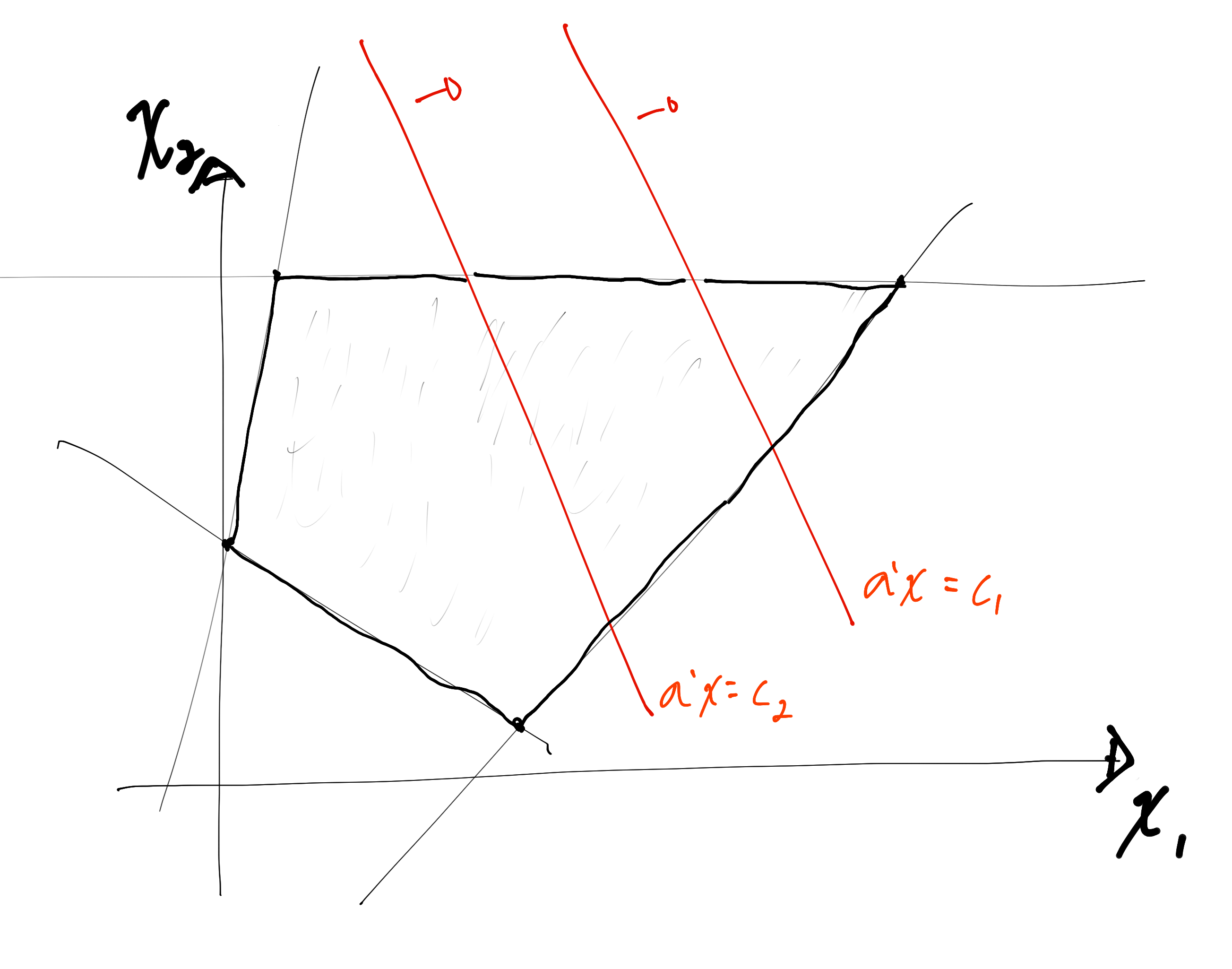
in the above case, the inequalities define a bounded region. You can see that making cost function \(a'x = c\) for a constant \(c\), we get an affine manifold (in \(\mathbb R^2\), those are just straight lines, in \(R^3\) they’d be planes, and so on), and the goal is to obtain the best \(c\) (minimum or maximum) for \(x\) delimited by the inequalities \(Ax \leq b\).

Pretty simple, isn’t it? It should be intuitive that the best result, if it exists (which it does in the above example), is to be found in one of the vertices of the delimited polyhedron (\(Ax \leq b\) doesn’t always delimit a polyhedron, but never mind tha). If that isn’t clear to you, maybe the following picture helps to vizualise

So, a simple algorithm would be to look vertex by vertex for the best one - and since we know the direction gradient of the cost function, we can do it in a strictly increasing way. If there are finitely many vertices (which’s usually the case), that shoud work.

What comes as a surprise is that it works well. You see, there could be a lot of vertices, so there’s no guarantee that your algorithm will be efficient. The surprise, is that, for most practical purposes, it works great. That was developed by the such as Dantzig and Kantorovich.

Convex Optimization

Linear programming problems are part of a more general class of optimization problems, the convex optimization problems: namely the ones in which the region of optimization is convex, and the cost function is convex as well.

A set \(S\) is convex just in the case that \(\alpha y + (1-\alpha)x \forall x,y \in S \forall \alpha \in [0,1]\). Intuitively, that condition asks that if \(x \in S\) and \(y \in S\), any points between \(x\) and \(y\) be also in \(S\).

Convex Cat

Non-convex Cat

Where non-convexity lies

Also, we say a function is convex just in case the above and including the graph of the function is convex. It should be easy to see that a linear function is convex - it’s in some sense the simplest convex set that there is.

A very special property of convex optimization problems is that they don’t have local-extremes - if you found a local maximum or minumum, you can be assured that it’s a global one.

That’s a very nice property to have, but that many real-world problems lack.

It’s very nice and satisfying when they do though. You’re guaranteed to make steady progress in the problem, with no backtracking. It seems some stories work like that - and I’m looking at you, shounen characters! Would be nice if life were like that, wouldn’t it? or would it? I’m not sure.

Next time well look at a more algebraic rendering of optimization, together with connexions with probability. Until then!